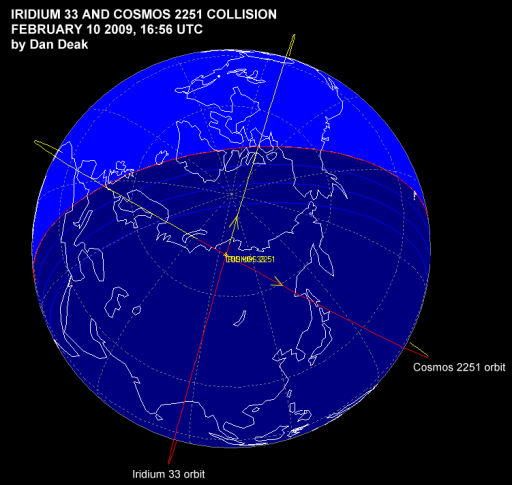
Orbital Collision
Wow. Talk about low-probability. An Iridium phone satellite (an active one) and a defunct soviet Cosmos satellite, both in polar orbits which were nearly perpendicular to one another, smacked into one another on Tuesday afternoon. That’s never, ever, ever happened before (no active satellites, or even defunct ones, have ever collided before). I mean, there’s a lot of room up there.
Of course, now you have over 500 pieces big enough to track (and who knows how many smaller bits of shrapnel below the 10cm mark), spinning round in a collection of orbits at a particularly useful altitude. And of course, if anything big enough to smash something hits that something, there’s another 500 pieces… they’ve had this as a nightmare scenario for a few decades now in the space sciences. It’s more likely that most of those bits will hit the atmosphere, slow down, fall in and burn up; but they’re somewhat worried that things like the ISS, the shuttle, the Hubble, or something equally valuable and irreplaceable might take a hit before then.
Now that is a bad Tuesday…

How would you calculate the probability of a thing like that? It seems very difficult, but then I start to think, it could actually be very simple.
If they both have clearly-defined orbits, then it should be possible to calculate, for each of them, exactly what its probability is of being at any given point at a particular instant.
And then you just multiply the two probabilities together, resulting in a very, very, very small number.
Would that be right?
Basicly, yes, that’s how you’d do it. There are complications (there’s a whole slew of academic papers on how to calculate this) and noone’s released an actual probability number for this collision that I’ve found, but the number was very, very small indeed. Problem now is, where you had two orbiting objects, you now have two orbiting clouds of debris, so the odds of a collision just went up quite a bit, and because it was a collision and so kinda messy, you’ve got those debris clouds spreading in random directions in both planes – so even the ISS, which is in a much higher orbit, hasn’t been ruled to be out of danger just yet. (The shuttle should be fine, but it’s not permanently in orbit so it’s easier for it to avoid trouble).